テトロミノ：４×５の長方形問題

　５種類のテトロミノ１個ずつを並べて４×５の長方形を作ることが不可能なのは、それぞれを市松模様に塗ると簡単に証明できます。

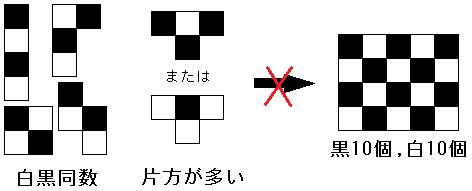
　４×５の長方形は、黒１０個と白１０個に塗り分けることができます。テトロミノの場合、５種類のうちの４つは黒２個と白２個になりますが、Ｔ字型のピースだけは黒３個と白１個（またはその逆）となり、白黒が同数になりません。

　これではどう並べても黒１０個と白１０個の図形にはなりません。つまり、４×５の長方形を作ることは不可能なのです。