テトロミノ
1×1の正方形(これを単位正方形と呼びます)4個を辺同士でつながるようにくっつけた物をテトロミノと言います。 この手のパズルでは5個つなげたペントミノが有名で色々な問題や文献があります。 それに比べてテトロミノはかなり少ないので、あえて取り上げてみました。
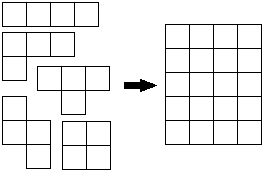 |
回転したり裏返したりして一致する物を同じとみなすと、テトロミノは全部で5種類あります。
その5種類を1個ずつ使って、単位正方形4×5の長方形に収めよという、有名な問題があります(左図)。 一見、どちらも単位正方形が20個なので並べ方を工夫すれば出来そうなのですが、実は不可能であることが 数学的に証明されています。 (証明はこちら) |
でも、この5種類を2個ずつ使うと5×8の長方形に収めることが可能で、 この形で株式会社テンヨーから発売されています(「テンヨー プラパズル」で検索すると出てきます)。
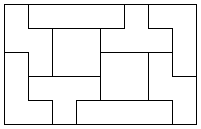
残念なことに、テンヨーのサイトでも5×8のケースに入れることしか紹介しておらず、他の問題はありません。 そこで、この5種類2個(計10個)で遊ぶ、私が考案したテトロミノの問題を次に紹介します(既にどこかで発表済みだとは思いますが)。
三倍体問題
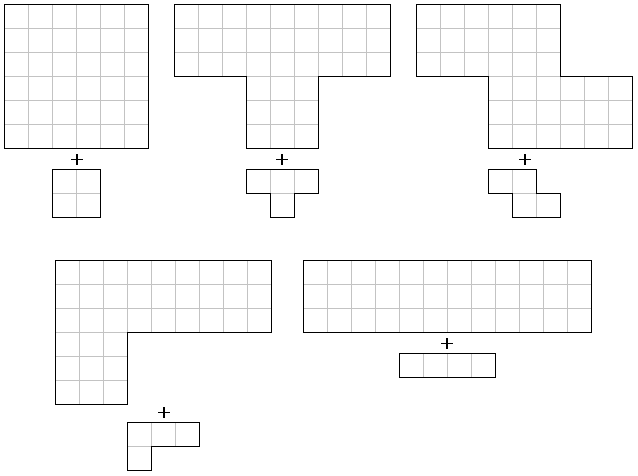
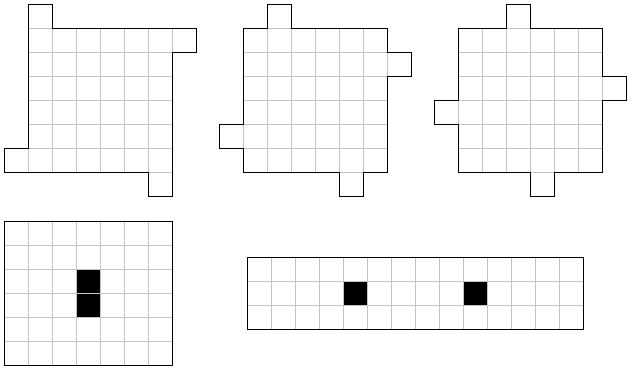
10個のピースから1個を抜いて、残りの9個で抜いたピースと同じ形で寸法が縦横3倍の形を作ります。
ピース穴あき問題
4×11の長方形内にピースの形の穴をあけ、残りの部分に10個のピースを収める問題です。 図の■の部分がピースを置かない空白部分です。
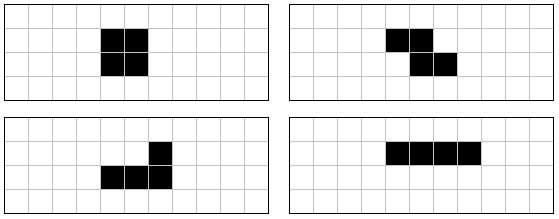
なお、T字型ピースの穴あきは不可能です。
その他の問題
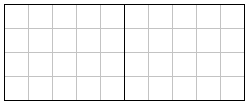 |
まず、4×10の長方形を作ってください。それができたら、次はちょうど真ん中で左右に分けられるように収め直してください。 |
図の■の部分はピースを置かない空白部分です。
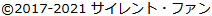

 メニューに戻る
メニューに戻る